DECISION TREES

Hello, welcome to my blog. Recently, I have been talking about classification. I have talked about a linear classifier, how to use logistic regression to learn coefficients for a linear classifier. Furthermore, I demonstrated how to implement logistic regression using the sci-kit learn library in Python and I talked about evaluation metrics for classifiers.

Today, I want to talk about another algorithm for classifying data – Decision Trees. This algorithm takes a different approach to classifying data which I will talk about in this post.

INTUITION BEHIND DECISION TREES

When making a difficult or important decision, we often consider or weigh the pros and cons of making a particular decision from a set of possible decisions. For example, consider a jobseeker who has to choose one job out of several job offers. He may decide to choose the job with the highest pay and benefits but what if that job required that he had to move to a different country that spoke a different language? He may decide to consider the second job that is closer to him but what if that job does not pay as much as the previous job? Finally, he may decide to take a job that with decent pay and benefits and also is not too far his friends and family. You can see that his decision on either accepting or rejecting a job offer was made by a series of small specific choices.

Concretely, the goal of decision tree modelling is to build a tree (from the data) that lets us make predictions about our data. This is done by splitting the data into two or more homogeneous sets based on the most significant feature in the data. The decision tree is ‘grown’ from data by continually splitting the data into as many homogeneous sets as possible until a stopping criterion is reached.

Decision trees are best suited for problems where the dependent variables are categorical or the relationship between the dependent and independent variable is non-linear. Although decision trees are best suited for classification problems, they can also be applied to regression problems as well. 

Before we go on let me mention some important terms associated with decision trees:

• Root node: This is the population or data we use to build the decision tree. This data gets subdivided into two or identical more sets.
• Splitting: This is the act of dividing a node into two or more sub-nodes.
• Pruning: The process of removing sub-nodes from a tree.
• Leaf/Terminal Node: This is a node that is not split on. These nodes are used for making predictions about our data.
• Decision Node: This is a sub-node that is split into two or more sub-nodes.

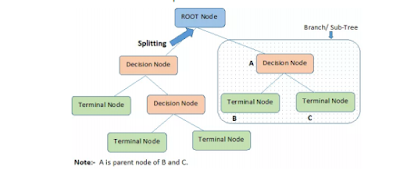Decision Tree Terminology

CRITERIA FOR SPLITTING

How do we decide the best feature to split on? The best feature is the feature that when split on gives the lowest classification error. This split results in the ‘purest’ or most ‘homogenous’ subset(s) of the data. There are various ways of measuring how ‘pure’ a split is. Some of them are

• Gini index: In this case we choose the feature which when split on results in a higher Gini score.
• Entropy: We choose the splitting feature as the one that results in the lowest entropy for a split.

STOPPING CRITERIA

Now that we know how to split our data. The next question is when do we stop splitting? There are three primary conditions:

1. When a feature split results in a homogeneous split. In this case we stop growing the tree because all the data points for that particular subset belong to the same target class so we don’t need to split that node.
2. There are no more features to split on.
3.  If the number of data-points in a node is too small. Making a split on such a node may result in predictions that may not be reliable. A good number is somewhere between 10 (for small data-sets) and 100 (for large data-sets).

MAKING PREDICTIONS

When a decision tree is fully ‘grown’ how do we make predictions with it? For a particular input x_i we traverse the grown tree using features of that input until we reach a leaf/terminal node where we make a prediction. The prediction at a leaf node is usually the majority class of data points in that leaf (for classification tasks) or the mean or median of the target class for data points in that leaf (for regression tasks).

ADVANTAGES

• The output of a decision tree model is easy to interpret for people without an analytical background. This is because its output can be reduced to a set of rules that can be used to make predictions. If a problem requires a model that can be easily interpreted, I recommend a decision tree.
• Decision trees can help us to quickly see or identify the relationship between two or more variables in the data. This is very useful in data exploration.
• Unlike regression that is sensitive to outliers and missing values, decision trees are quite capable of handling such problems. The learning algorithm for a decision tree can be modified to take into account the presence of missing data so it can ‘decide’ what to do when it encounters missing data.

Perhaps the most important disadvantage of decision trees is that it is prone to over-fitting. This can be controlled by adding extra stopping conditions to the decision tree’s learning algorithm to combat over-fitting.

 STOPPING CONDITIONS TO COMBAT OVERFITTING

• Limiting the depth of the tree. When we split on a feature the depth of the tree increases. If a tree is grown too deep it may learn relationships that are very specific to the training data which will cause it to fail to generalize well on future data. This is because by design splitting on a feature reduces the classification error. So we if keep splitting on features, the depth of the tree increases which will reduce the training error but it may give us a tree that overfits the training data.
• Reduction in classification error. If a particular split on a node does not significantly improve the classification error we stop splitting on that node and make that node a leaf/terminal node. This may be useful sometimes but this approach is short-sighted because it may cause us to miss out a future split that may result in a considerable reduction in training error.

PRUNING

This is a solution to the problem for stopping condition (ii) above. To implement this, we first grow a very complex tree and then remove (or prune) leaves that do not give us significant improvement of the classification error. This reduces the depth of the complex tree which reduces the risk of overfitting.

SUMMARY

In this post, I introduced another algorithm for classification – Decision trees. I talked about the procedure for growing a tree and methods for preventing over-fitting in decision trees. Thank you once again for visiting my blog. I encourage you to leave a comment about this post or any other post. If you have a question I will do my best to answer it. Don’t forget to add your email to this blog’s mailing list if you have not. Until next time. Cheers!!!