IMPLEMENTING LINEAR REGRESSION USING PYTHON

Hello once again. Welcome to my blog. In the last post I introduced linear regression which is a powerful tool used to find the relationship between a response variable and one or more explanatory variables. In this post, I will demonstrate how to implement linear regression using a popular programming language – Python. To perform linear regression in Python I will make use of libraries. You can think of them as plug-ins that are used to add extra functionality to Python. The libraries I will be using are as follows:

i.                    Pandas (for loading data)

ii.                  Numpy (for arrays)

iii.                Statsmodels.api & Statsmodels.formula.api (for linear regression)

iv.                 Matplotlib (for visualization)

For this demonstration, I will use the King County House Sales data to predict the price (in dollars) of house using just one feature – square footage of the house. This dataset contains information about houses sold in King County (a region in Seattle). This dataset is public and can be accessed by anyone (I think a Google search should provide a link to where you can download it from). It’s in a CSV format (CSV stands for comma separated values). To load the dataset we use the Pandas library. Once we have loaded the dataset we can now use it to perform linear regression.

MACHINE LEARNING ALGORITHMS – LINEAR REGRESSION

Hello once again. How has your week been? Hope it has been good. Thanks for visiting my blog once again. Today I would like to talk about one of the most popular and useful machine learning algorithms – Linear Regression.

First, what is regression? Regression basically describes the relationship between numbers. For example, there is a relationship between height (a number) and weight (another number). Generally, weight tends to increase with height. Formally, regression is concerned with identifying the relationship between a single numeric variable (called the dependent variable, response or outcome) we are interested in and one or more variables (called the independent variable or predictors). If there is only a single independent variable, this is called simple linear regression, otherwise it’s known as multiple linear regression.

What we assume in regression is that the relationship between the independent variable and the dependent variable follows a straight line. It models this relationship using the equation below:

                 y = a + bx 

Where,

y – the dependent variable

a – intercept, this is the value of y when x = 0

b – slope, this is how much y changes for an increment in the value of x

How Regression works

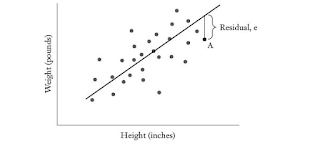
The goal of regression is to find a line that best fits our data. Let me illustrate with the following scatterplot showing the relationship between height (in inches) and weight (in pounds)

From the scatterplot, it can be seen that weight generally increases with height and vice-versa. Now how do we find the line that best fits this data? This is done by finding the line has the lowest sum of squared residuals. Let me explain, the equation for y shown above generates the predicted value for y which will differ from the actual value of y by some value (called residual or error). This value is squared and summed for all points in our data and a line that has the lowest sum of squared errors is chosen. This is done by adjusting the values of a and b to values such that they gives a line that fits our data. Let’s show the same data fitted with the line of best of fit.

Although the fitted line does not pass through each point in the data, it does a pretty good job of capturing the trend in our data.

How to choose a and b

Earlier on I said we choose line with a and b such that it gives the lowest sum of squared errors. How exactly do we do this? There are three ways:

1. Ordinary least squares estimation.
2. Gradient descent.
3. The normal equation.

I won’t go in depth in describing this methods but a Google search for any of these terms will give you more information if you are interested in knowing more about them.

Congratulations!!! Now you know about linear regression one of the most powerful tools in machine learning. In the next post, I will demonstrate how to perform linear regression using a popular programming language – Python. If you have a question please feel free to drop a comment.

Thanks once again for visiting my blog, hope you have a wonderful and productive week ahead. Cheers. 

WHAT IS MACHINE LEARNING

WHAT IS MACHINE LEARNING?

Hello everyone! Happy new year to you all. Sorry for the delay in making this post, just started NYSC for real and believe me it's quite stressful but there have fun times too (I guess). Anyway, enough chit-chat let's get to the topic of the day - What is machine learning? This for me is a good place to start for anyone who has an interest in any topic (not just machine learning). What really is the thing I am interested in? That's the first question that I feel should be clearly answered. The objective of the post is to briefly define machine learning and give some of its popular applications.

According to Wikipedia, machine learning explores the study and construction of algorithms that can learn to make predictions from data rather than following static program instructions. Let me explain, machine learning uses data to make predictions. These predictions could be anything from the saying what the weather will be tomorrow, to classifying a handwritten digit, recognizing a picture or predicting what the price of an item will be given features of said item.

All of the tasks just mentioned would be difficult to achieve using rigid programming rules. For example, a classic problem in machine learning is classification of hand-written digits. Suppose we wanted to define what the digit '7' should look like, how would we do that? This would be difficult to do because people have different ways of writing the number '7'. Trying to write rules to define what the digit '7' is (or isn't) to a program would be difficult. In this case, the best option would be for the program to 'learn' the various parameters required to correctly classify a digit. To do this, we would collect samples of hand-written digits (data) which we would now feed to a machine learning algorithm. The output of this algorithm can now be used to classify digits.

Now that you know what machine learning is, let's look at some of its major uses (if you feel there others, please feel free to add them in the comments section). Machine learning is used mainly for prediction like I mentioned earlier. This can be further classified into:

i.                    Regression

ii.                  Classification

In regression, we use numbers to predict numbers. Let me use the popular example of trying to predict the price of a house. Assume we trying to predict the price of a house and that we also features (also called attributes) of this house e.g. square footage, number of bedrooms, number of bathrooms, the year it was built and so on. The task is given all these features (which are basically numbers) can predict how much this house will sell for? (another number).

Classification is more like regression – the only difference in this case is that we are trying to predict a class. Another popular example for classification is spam filtering where we use features of an email such the words in the email, sender’s name, sender’s IP address etc. to predict if the email is spam or not. This is called binary classification because we trying to predict which of two classes an email (or the item to be classified) belongs to. Sometimes, there may be more than two classes. In this case it’s called multi-class classification. A good example is classification of hand-written digits where we try to predict if a digit belongs of 1 out of a possible 10 classes.

Another application of machine learning I would to mention is in the area of products recommendation. This application is used by extensively by companies such as Amazon (to recommend what shoppers may like to buy) and Netflix (to recommend movies to users). Machine learning also finds application in areas such as image recognition and classification where neural networks are used to recognize and /or classify an image.

I hope this post has clearly explained what machine learning is and its application. Please feel free to drop a comment about anything that is unclear to you. Thanks for reading my blog. Hope to see you soon.  Cheers!!!