Hello, welcome to my blog. In my previous post I introduced another
classification algorithm called decision trees. In this post I want to
demonstrate how to implement decision trees using the scikit-learn library in
Python.
For this demonstration, I will be using the LendingClub
dataset. LendingClub is a peer-to-peer lending company that directly connects
borrowers and potential lenders/investors. The goal of this demonstration is to
build a decision tree classification model that will predict whether or not a
loan provided by LendingClub is likely to default. The dataset contains records
of about 120,000 loans granted by LendingClub.
The dataset is in SFrame format so I will use the ‘SFrame’ function
from GraphLab to load the data. Feel free to use the stand alone ‘sframe’
library to load the data. Like I mentioned earlier I will use the scikit-learn
library to build a decision tree model from the LendingClub data. The full code
for this demonstration will be given at the end of this post, here I will just
display screenshots of the results of the program.
PRELIMINARY STEPS
The dataset has a disproportionally large amount of safe
loans (about 80% of the loans in the dataset are safe loans). This presents a
problem because it could lead to misleading information about the performance
of the classifier. In order to combat this problem, I undersampled the majority
class so that the distribution of safe and unsafe loans was approximately equal
for both classes. This is a crude method of handling imbalanced classes because
we are throwing away data points which is not always a good idea. Read this
excellent post for other ideas you can try.
Next, I converted the categorical variables in the data to
binary features via one-hot encoding. This is because scikit-learn’s decision
tree implementation requires numerical values for the data you give it. Finally,
I split the data into training (80%) and test (20%) sets and used a random seed
to ensure reproducibility.
TRAINING THE DECISION TREE MODEL
To create a decision tree model, I simply created an object
of the sklearn.tree.DecisionTreeClassifier class. I specified max_depth = 2 so
that I can easily visualize and interpret the decision tree. Obviously it would
be easier to visualize and explain a small tree compared to a very large and
complex tree. I used the ‘fit’ method to fit a decision tree model on the
training data.
VISUALIZING THE TREE
We can get a visual representation of the decision tree using
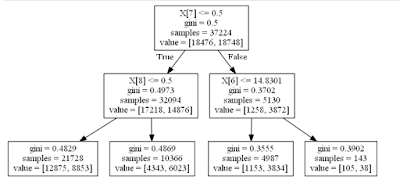
scikit-learn and the Graphviz package. Below is a picture of the decision tree
that was grown from the LendingClub dataset
Interpreting the Decision Tree
The first split was made on X[7] which is the feature grade.A
(this column has a value of 1 if the loan was a grade A loan or 0 if it wasn’t).
The left side of this split are the loans that were not grade A loans which
amount to 32,094 of the 37,224 training examples. From this node another split
was made on X[8] which is the feature grade.B. On the left side of this split i.e.
loans that were not grade A and grade B loans 12,875 of these loans were unsafe
while 8,853 of these loans were safe. On the right side of this split i.e.
loans that were not grade A loans but grade B loans 4,343 of these loans were
unsafe while 6,023 of these loans were considered to be safe.
Going back to the first split on X[7], the right side of this
split represent loans that were grade A loans which represent 5,130 of the
37,224 training examples. From this node another split was made on X[6] which
is the total late fees received for the loan. On the left side of this split
i.e. loans with X[6] less than or equal to 14.8301 and also grade A loans,
1,153 of these loans were unsafe while 3,834 of the were safe. On the right
side of this split i.e. grade A loans with X[6] greater than 14.8301, 105 were
unsafe while 38 were safe.
Since we are predicting the majority class (this is a classification
problem), we can classify a loan as safe or unsafe using the following rules:
- If grade.A = 0 and grade.B = 0 then loan is unsafe.
- If grade.A = 0 and grade.B = 1 then loan is safe.
- If grade.A = 1 and total_rec_late_fee <= 14.8301 then loan is safe.
- If grade.A = 1 and total_rec_late_fee > 14.8301 then loan is unsafe.
EVALUATING THE DECISION TREE
I evaluated the performance of the decision tree on test data
using the ‘score’ method. The model had an accuracy of 62% on the test data. This
indicates that the tree is fairly good at discriminating safe loans from unsafe
loans. One of the things that slightly hampered the performance of the tree is
the ‘max_depth’ parameter. Increasing this parameter will improve the
performance of tree on test data although it should not be too large in order
to avoid overfitting.
ASIDE
While working on this blog post, I noticed the ‘purpose’
column in the dataset which represents the reason why the borrower is taking
the loan. I wondered if there was any relationship between the purpose of a
loan and whether the borrower defaulted on the loan or not. This is something I
feel is worth investigating and I will report my results on this blog when I do
that.
I also want to announce that I have created a GitHub repository that has my implementation of gradient descent (for linear
regression) and gradient ascent for (logistic regression). More projects will
added to the repository very soon.
SUMMARY
In this blog post, I demonstrated how to implement decision
trees using the scikit-learn library in Python. Thank you once again for
reading this post. If you have any question about this post or any other post
leave a comment and I will do my best to answer you. Once again I urge you to
subscribe to my blog posts in case you have not done so. Enjoy the rest of your
weekend. Cheers!!!
Code for decision trees
#import needed libraries
import numpy as np
import graphlab as gl #The data in sframe format
import sklearn.tree
#Load the dataset
loans = gl.SFrame('lending-club-data.gl/')
#Check the number of rows and columns in the data
print loans.shape
#Recode the 'bad_loans' column in a more intuitive way
loans['safe_loans'] = loans['bad_loans'].apply(lambda x: +1 if x==0 else -1)
loans.remove_column('bad_loans')
#proportion of safe loans and risky loans
print "Number of safe loans: ", np.sum(np.array(loans['safe_loans'] == +1)) /float(len(loans))
print "Number of risky loans: ", np.sum(np.array(loans['safe_loans'] == -1)) /float(len(loans))
#Extract subset of features from the dataset
features = ['grade', # grade of the loan
'sub_grade', # sub-grade of the loan
'short_emp', # one year or less of employment
'emp_length_num', # number of years of employment
'home_ownership', # home_ownership status: own, mortgage or rent
'dti', # debt to income ratio
'purpose', # the purpose of the loan
'term', # the term of the loan
'last_delinq_none', # has borrower had a delinquincy
'last_major_derog_none', # has borrower had 90 day or worse rating
'revol_util', # percent of available credit being used
'total_rec_late_fee', # total late fees received to day
]
target = 'safe_loans' # prediction target (y) (+1 means safe, -1 is risky)
# Extract the feature columns and target column
loans = loans[features + [target]]
safe_loans_raw = loans[loans[target] == +1]
risky_loans_raw = loans[loans[target] == -1]
print "Number of safe loans : %s" % len(safe_loans_raw)
print "Number of risky loans : %s" % len(risky_loans_raw)
# Since there are fewer risky loans than safe loans, find the ratio of the sizes
# and use that percentage to undersample the safe loans.
percentage = len(risky_loans_raw)/float(len(safe_loans_raw))
risky_loans = risky_loans_raw
#Sample this percentage from the safe_loans data
#setting seed for reproducibility
safe_loans = safe_loans_raw.sample(percentage, seed=1)
# Append the risky_loans with the downsampled version of safe_loans
loans_data = risky_loans.append(safe_loans)
#Check the proportion of safe and risky loans to ensure they are about the same
#proportion of safe loans and risky loans
print "Number of safe loans: ", np.sum(np.array(loans_data['safe_loans'] == +1)) /float(len(loans_data))
print "Number of risky loans: ", np.sum(np.array(loans_data['safe_loans'] == -1)) /float(len(loans_data))
#Function to perform one-hot encoding for categorical variables
categorical_variables = []
for feat_name, feat_type in zip(loans_data.column_names(), loans_data.column_types()):
if feat_type == str:
categorical_variables.append(feat_name)
for feature in categorical_variables:
loans_data_one_hot_encoded = loans_data[feature].apply(lambda x: {x: 1})
loans_data_unpacked = loans_data_one_hot_encoded.unpack(column_name_prefix=feature)
# Change None's to 0's
for column in loans_data_unpacked.column_names():
loans_data_unpacked[column] = loans_data_unpacked[column].fillna(0)
loans_data.remove_column(feature)
loans_data.add_columns(loans_data_unpacked)
#Split data into train and test data
train_data, test_data = loans_data.random_split(.8, seed = 1)
featuresList = loans_data.column_names()
#Remove target column 'safe_loans' from featuresList
featuresList.remove('safe_loans')
#Index using our features list to create the training and test sets
pred_train = train_data[featuresList]
pred_test = test_data[featuresList]
#Do the same for the target column
target_train = train_data['safe_loans']
target_test = test_data['safe_loans']
#Convert them to numpy arrays
pred_train = pred_train.to_numpy()
pred_test = pred_test.to_numpy()
target_train = target_train.to_numpy()
target_test = target_test.to_numpy()
#Let's train a decision tree classifer with max_depth = 2
treeClassifier = sklearn.tree.DecisionTreeClassifier(max_depth=2)
#Fit classifier on the training data
decision_tree_model = treeClassifier.fit(pred_train, target_train)
#Visualizing the tree
from io import BytesIO as StringIO
from IPython.display import Image
out = StringIO()
sklearn.tree.export_graphviz(decision_tree_model, out_file=out)
import pydotplus
graph=pydotplus.graph_from_dot_data(out.getvalue())
Image(graph.create_png())
#Evaluating the tree
#the score function gives us the accuracy of the decision tree model
print "Accuracy of decision tree on test data: %.3f" % decision_tree_model.score(pred_test, target_test)
#Accuracy of decision tree on test data: 0.619
No comments:
Post a Comment